Junsu Pan

I received my Ph.D. in economics from UNC-Chapel Hill. My research interests are financial econometrics and machine learning.

“Tensor PCA for Factor Models”

A brief introduction:

A traditional factor model aims to explain the co-movements of large number of variables (observable) with only a few factors (unobservable). For example, a collection of large number of asset returns can be explained by a small number of “risk factors” which includes, e.g., the market risk, firm size risk, book-market ratio risk, and so on. The intuition is that holding each asset should be compensated based on how risky it is, a more risky asset should be expected to pay higher returns for holding such risks, and this is called “risk premium”. In factor models, “factor loadings” are the coefficients that capture the cross-sectional heterogeneity. In the asset returns example, they measure the level of risk for each asset.

To visualize a factor model:

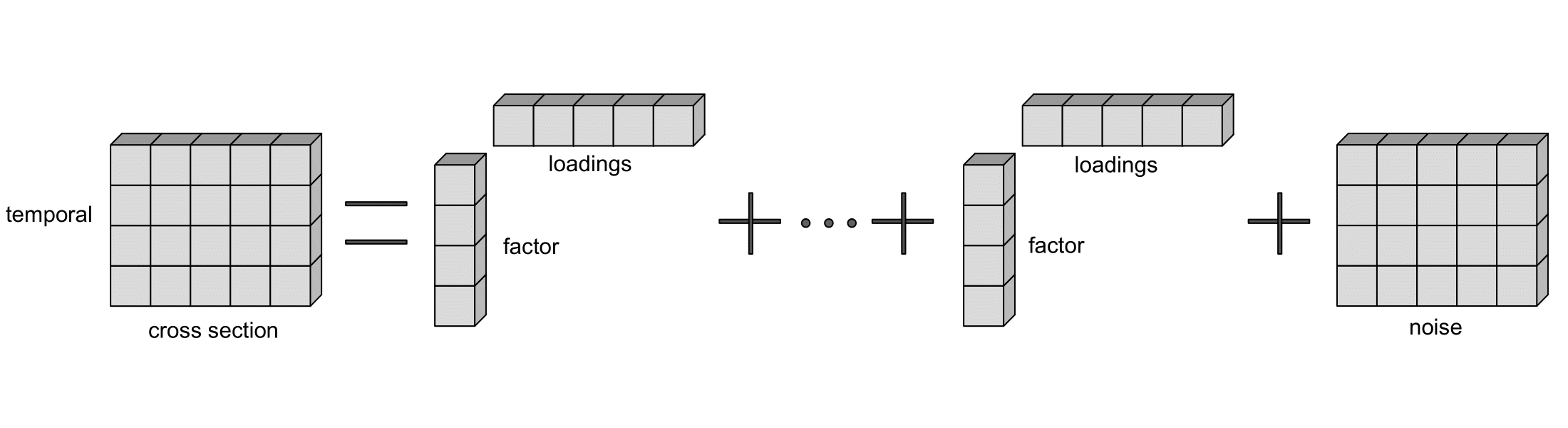
However, traditional factor models can only be applied to matrices (panel data), which only has two dimensions - temporal and cross-section. What happens if the data is of more than two dimensions, i.e., a tensor?

A tensor is a higher dimensional array - an extension of vectors and matrices:

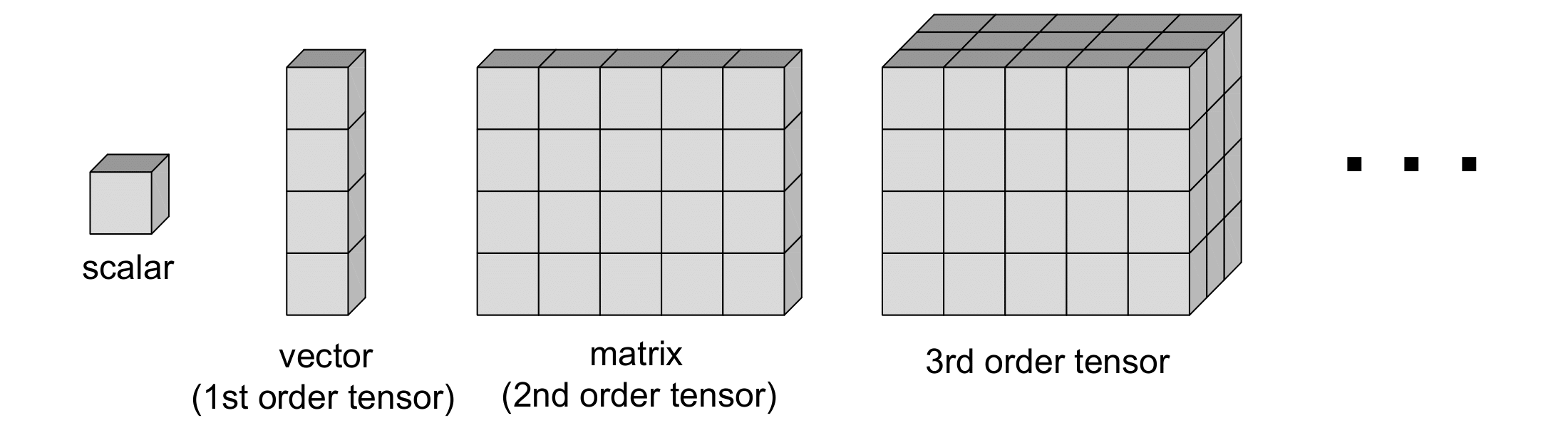
Examples:

• Macro Data: panel of macro indicators + regional dimension
• Sales Data: panel of firms selling products through time

Then a factor model for a 3rd order tensor would look like:

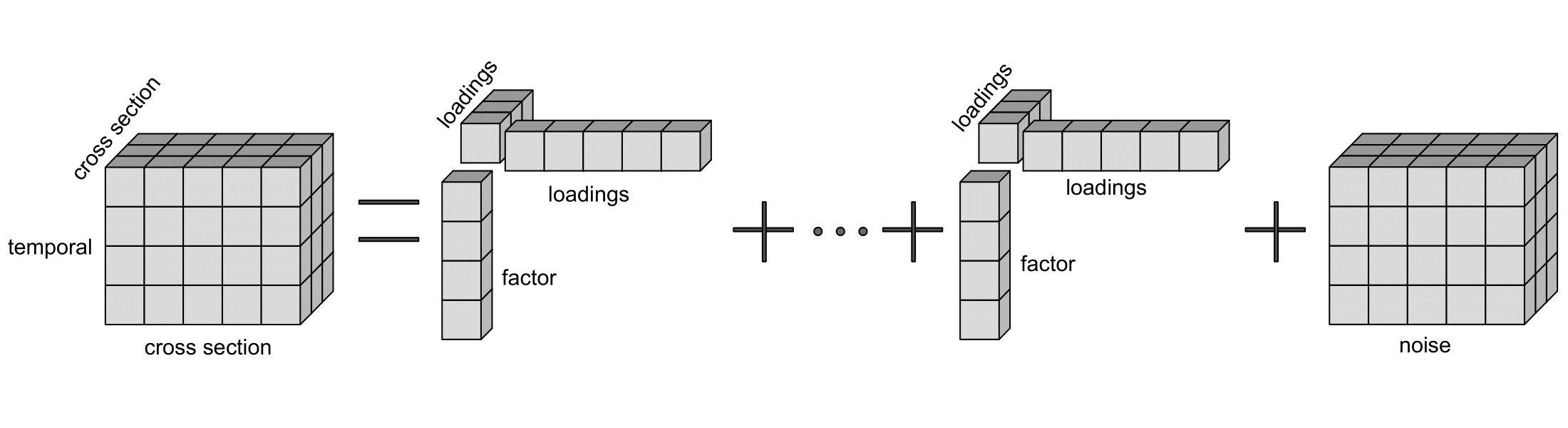
We developed the factor model for any d-dimensional tensors which is an extension of the traditional factor models, and it is called tensor factor model.

The benefits of using tensor factor model:

1. it allows to identify the loadings associated with the additional dimensions,
2. the theory and simulations show improved estimation accuracy with more tensor dimensions,
3. model complexity (# of parameters) is significantly reduced compared to traditional one when you have a tensor data.

For estimation of the tensor factor model, we designed an algorithm that is called Tensor Principal Component Analysis (TPCA).

The advantages of TPCA:

1. easy to use in practice: based on PCA,
2. closed-form estimators, avoids non-convex optimization,
3. allows sequential computation of factors.

To read more about this algorithm, the theoretical results, the hypothesis test for selecting number of factors, Monte Carlo simulations, and an empirical application, please click here to download the paper. To estimate your own tensor factor model, click here to install the Python package.